Below you will find a general outline of the sixth major formulation of the repetition spacing algorithm used in SuperMemo. It is referred to as Algorithm SM-8 since it was first implemented in SuperMemo 8. Although the increase in complexity of Algorithm SM-8 as compared with its predecessor, Algorithm SM-6, is incomparably greater than the expected benefit for the user, there is a substantial theoretical and practical evidence that the increase in the speed of learning resulting from the upgrade may fall into the range from 30 to 50%. Note that a newer version of the algorithm exists: Algorithm SM-11.

Algorithm SM-8

SuperMemo computes optimum inter-repetition intervals from the grades scored by individual items in learning. This record is used to estimate the current strength of a given memory and the difficulty of the underlying item. This difficulty expresses complexity of memories and the effort needed to produce unambiguous and stable memory traces. SuperMemo takes the requested recall rate as the optimization criterion (e.g. 95%), and computes the intervals that satisfy this criterion. The function of optimum intervals is represented in a matrix form (OF matrix) and is subject to modification based on the results of the learning process.

This is a more detailed description of the Algorithm SM-8:

1. Inter-repetition intervals are computed using the following formula:

   I(1)=OF[1,L+1]
   I(n)=I(n-1)*OF[n,AF]

   where:

   • OF - matrix of optimal factors, which is modified in the course of repetitions
   • OF[1,L+1] - value of the OF matrix entry taken from the first row and the L+1 column
   • OF[n,AF] - value of the OF matrix entry that corresponds with the n-th repetition, and with item difficulty AF
   • L - number of times a given item has been forgotten (from "memory Lapses")
   • AF - number that reflects absolute difficulty of a given item (from "Absolute difficulty Factor")
   • I(n) - n-th inter-repetition interval for a givent item 

2. The matrix of optimal factors OF used in Point 1 has been derived from the mathematical model of forgetting and from similar matrices built on data collected in years of repetitions in collections created by a number of users. Its initial setting corresponds with values found for a less-than-average student. During repetitions, upon collecting more and more data about the student’s memory, the matrix is gradually modified to make it approach closely the actual student’s memory properties. After years of repetitions, new data can be fed back to generate more accurate initial matrix OF. In SuperMemo 2000, this matrix can be viewed in 3D with Tools : Statistics : Analysis : 3-D Graphs : O-Factor Matrix
3. The absolute item difficulty factor (A-Factor), denoted AF in Point 1, expresses the difficulty of an item (the higher it is, the easier the item). It is worth noting that AF=OF[2,AF]. In other words, AF denotes the optimum interval increase factor after the second repetition. This is also equivalent with the highest interval increase factor for a given item. Unlike E-Factors in Algorithm SM-6 employed in SuperMemo 6 and SuperMemo 7, A-Factors express absolute item difficulty and do not depend on the difficulty of other items in the same collection of study material
4. Optimum values of the entries of the OF matrix are derived through a sequence of approximation procedures from the RF matrix which is defined in the same way as the OF matrix (see Point 1), with the exception that its values are taken from the real learning process of the actual student. Initially, matrices OF and RF are identical; however, entries of the RF matrix are modified with each repetition, and a new value of the OF matrix is computed from the RF matrix by using approximation procedures. This effectively produces the OF matrix as a smoothed up form of the RF matrix. In simple terms, the RF matrix at any given moment corresponds to its best-fit value derived from the learning process; however, each entry is considered a best-fit entry on it’s own, i.e. in abstraction from the values of other RF entries. At the same time, the OF matrix is considered a best-fit as a whole. In other words, the RF matrix is computed entry by entry during repetitions, while the OF matrix is a smoothed copy of the RF matrix
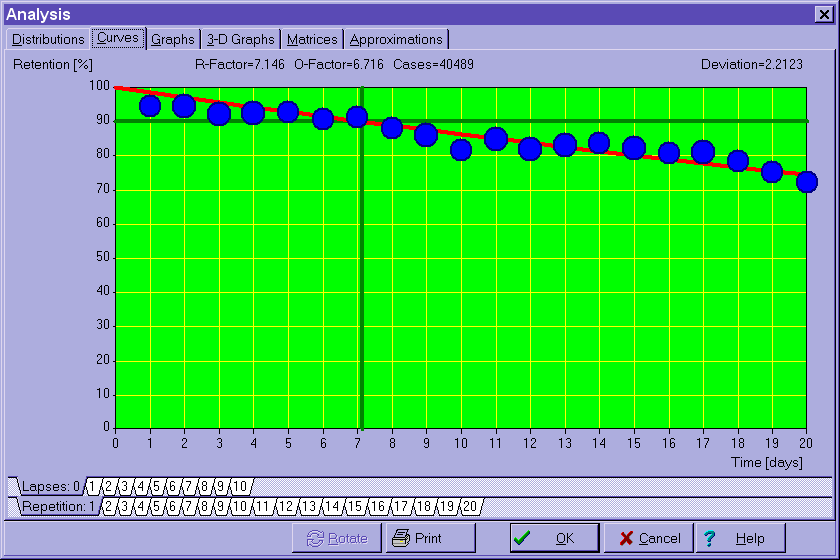
5. Individual entries of the RF matrix are computed from forgetting curves approximated for each entry individually. Each forgetting curve corresponds with a different value of the repetition number and a different value of A-Factor (or memory lapses in the case of the first repetition). The value of the RF matrix entry corresponds to the moment in time where the forgetting curve passes the knowledge retention point derived from the requested forgetting index. For example, for the first repetition of a new item, if the forgetting index equals 10%, and after four days the knowledge retention indicated by the forgetting curve drops below 90% value, the value of RF[1,1] is taken as four. This means that all items entering the learning process will be repeated after four days (assuming that the matrices OF and RF do not differ at the first row of the first column). This satisfies the main premise of SuperMemo, that the repetition should take place at the moment when the forgetting probability equals 100% minus the forgetting index stated as percentage. In SuperMemo 2000, forgetting curves can be viewed with Tools : Statistics : Analysis : Curves:
   
6. The OF matrix is derived from the RF matrix by: (1) fixed-point power approximation of the R-Factor decline along the RF matrix columns (the fixed point corresponds to second repetition at which the approximation curve passes through the A-Factor value), (2) for all columns, computing D-Factor which expresses the decay constant of the power approximation, (3) linear regression of D-Factor change across the RF matrix columns and (4) deriving the entire OF matrix from the slope and intercept of the straight line that makes up the best fit in the D-Factor graph. The exact formulas used in this final step go beyond the scope of this illustration.
   Note that the first row of the OF matrix is computed in a different way. It corresponds to the best-fit exponential curve obtained from the first row of the RF matrix.
   All the above steps are passed after each repetition. In other words, the theoretically optimum value of the OF matrix is updated as soon as new forgetting curve data is collected, i.e. at the moment, during the repetition, when the student, by providing a grade, states the correct recall or wrong recall (i.e. forgetting) (in Algorithm SM-6, a separate procedure Approximate had to be used to find the best-fit OF matrix, and the OF matrix used at repetitions might differ substantially from its best-fit value)
7. The initial value of A-Factor is derived from the first grade obtained by the item, and the correlation graph of the first grade and A-Factor (G-AF graph). This graph is updated after each repetition in which a new A-Factor value is estimated and correlated with the item’s first grade. Subsequent approximations of the real A-Factor value are done after each repetition by using grades, OF matrix, and a correlation graph that shows the correspondence of the grade with the expected forgetting index (FI-G graph). The grade used to compute the initial A-Factor is normalized, i.e. adjusted for the difference between the actually used interval and the optimum interval for the forgetting index equal 10%
8. The FI-G graph is updated after each repetition by using the expected forgetting index and grade values. The expected forgetting index can easily be derived from the interval used between repetitions and the optimum interval computed from the OF matrix. The higher the value of the expected forgetting index, the lower the grade. From the grade and the FI-G graph (see FI-G graph in Analysis), we can compute the estimated forgetting index which corresponds to the post-repetition estimation of the forgetting probability of the just-repeated item at the hypothetical pre-repetition stage. Because of the stochastic nature of forgetting and recall, the same item might or might not be recalled depending on the current overall cognitive status of the brain; even if the strength and retrievability of memories of all contributing synapses is/was identical! This way we can speak about the pre-repetition recall probability of an item that has just been recalled (or not). This probability is expressed by the estimated forgetting index
9. From (1) the estimated forgetting index, (2) length of the interval and (3) the OF matrix, we can easily compute the most accurate value of A-Factor. Note that A-Factor serves as an index to the OF matrix, while the estimated forgetting index allows one to find the column of the OF matrix for which the optimum interval corresponds with the actually used interval corrected for the deviation of the estimated forgetting index from the requested forgetting index

To sum it up. Repetitions result in computing a set of parameters characterizing the memory of the student: RF matrix, G-AF graph and FI-G graph. They are also used to compute A-Factors of individual items that characterize the difficulty of the learned material. The RF matrix is smoothed up to produce the OF matrix, which in turn is used in computing the optimum inter-repetition interval for items of different difficulty (A-Factor) and different number of repetitions (or memory lapses in the case of the first repetition). Initially, all student’s memory parameters are taken as for a less-than-average student, while all A-Factors are assumed to be equal

Optimization solutions used in Algorithm SM-8 have been perfected over 10 years of using the SuperMemo method with computer-based algorithms (first implementation: December 1987). This makes sure that the convergence of the starting memory parameters with the actual parameters of the student proceeds in a very short time. Similarly, the introduction of A-Factors and the use of the G-AF graph greatly enhanced the speed of estimating individual item difficulty. The adopted solutions are the result of constant research into new algorithmic variants. The postulated employment of neural networks in repetition spacing is not likely to compete with the presented algebraic solution. Although it has been claimed that Algorithm SM-6 is not likely to ever be substantially improved (because of the substantial interference of daily casual involuntary repetitions with the highly tuned repetition spacing), the initial results obtained with Algorithm SM-8 are very encouraging and indicate that there is a detectable gain at the moment of introducing new material to memory, i.e. at the moment of the highest workload. After that, the performance of Algorithms SM-6 and SM-8 is comparable. The gain comes from faster convergence of memory parameters used by the program with actual memory parameters of the student. The increase in the speed of the convergence was achieved by employing actual approximation data obtained from students who used SuperMemo 6 and/or SuperMemo 7

Algorithm SM-8 is constantly being perfected in successive releases of SuperMemo, esp. to account for newly collected repetition data, convergence data, input parameters, etc.

If you would like your own software to use the Algorithm SM-8, read about SM8OPT.DLL

Frequently Asked Questions

(Zoran Maximovic, Serbia, Sep 25, 2000)
Question:
In approximation graphs in Tools : Statistics : Analysis, some of the curves "jump out" of the graph area. What is wrong?
Answer:
This was a harmless bug in the algorithm in SuperMemo 98/99. The assumption is that intervals cannot grow beyond the value of A-Factor. For that reason, the maximum R-Factor should equal the relevant A-Factor. However, in plotting the forgetting curves, higher values of U-Factors are used as repetitions may be delayed (e.g. with Mercy, user procrastination, etc.). The algorithm puts a cap on the maximum R-Factor value (along the theoretical assumption that R-Factors cannot be greater than corresponding A-Factors). However, the implementation used the maximum U-Factor value as the cap (the one used in plotting the forgetting curve). Consequently, R-Factors could grow larger than A-Factors and the curve would "jump out" of the graph, which displays the correct cap.
This bug should have little effect on the learning process. The higher cap does not invalidate the correctness of R-Factors. It just does not prevent very long intervals in case of very good repetition results.

This bug has been fixed in SuperMemo 2000